Many people think of the Yamaha Montage as an FM synth and a sample based (AWM) synth. But if you own an FM synth like the Yamaha Montage then you also own an synth with additive synthesis capabilities.
A typical waveform is the square wave. A square wave is just all of the odd partials add 1/N amplitudes. So, the fundamental has a relative amplitude of 1.0. All even partials have a relative amplitude of 0 so we can skip those. The 3rd partial has a relative amplitude of 1/3 (0.33), the 5th partial is 1/5 (0.20), the 7th partial at (1/7) 0.14, the 9th partial at (1/9) 0.11, the 11th partial at 1/11 (0.09) , the 13th at 1/13 (0.08), the 15th at 1/15 (0.07) etc.
I used algorithm 1 which is all 8 operators as carriers.

Then set the relative frequency and levels as follows:
| Operator | Frequency | Level |
| 1 | 1.00 | 99 |
| 2 | 3.00 | 33 |
| 3 | 5.00 | 20 |
| 4 | 7.00 | 14 |
| 5 | 9.00 | 11 |
| 6 | 11.00 | 9 |
| 7 | 13.00 | 8 |
| 8 | 15.00 | 7 |
But the result sounded nothing like a square wave! In fact, when I looked at the output, it looked like this:
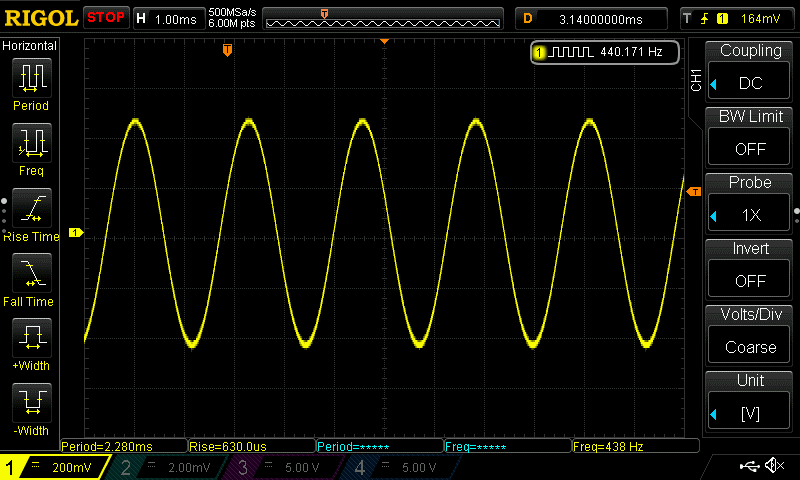
Which you can see is just a simple sine wave!
It turns out that the operator levels are not linear but exponential. Here are the relative measurements I measured the AC voltage of the single operator output at 440Hz and normalized the results.
| Op Lvl | Normalized Magnitude |
| 99 | 100.000 |
| 98 | 92.000 |
| 97 | 84.400 |
| 96 | 77.300 |
| 95 | 70.900 |
| 94 | 65.290 |
| 93 | 59.880 |
| 92 | 54.920 |
| 91 | 50.360 |
| 90 | 46.190 |
| 89 | 42.360 |
| 88 | 38.840 |
| 87 | 35.610 |
| 86 | 32.650 |
| 85 | 29.940 |
| 84 | 27.460 |
| 83 | 25.180 |
| 82 | 23.080 |
| 81 | 21.150 |
| 80 | 19.400 |
| 79 | 17.790 |
| 78 | 16.310 |
| 77 | 14.950 |
| 76 | 13.710 |
| 75 | 12.560 |
| 74 | 11.520 |
| 73 | 10.560 |
| 72 | 9.670 |
| 71 | 8.860 |
| 70 | 8.130 |
| 69 | 7.450 |
| 68 | 6.820 |
| 67 | 6.250 |
| 66 | 5.730 |
| 65 | 5.250 |
| 64 | 4.810 |
| 63 | 4.400 |
| 62 | 4.040 |
| 61 | 3.700 |
| 60 | 3.390 |
| 59 | 3.100 |
| 58 | 2.840 |
| 57 | 2.600 |
| 56 | 2.380 |
| 55 | 2.180 |
| 54 | 2.000 |
| 53 | 1.830 |
| 52 | 1.670 |
| 51 | 1.530 |
| 50 | 1.400 |
| 49 | 1.280 |
| 48 | 1.180 |
| 47 | 1.070 |
| 46 | 0.980 |
| 45 | 0.900 |
| 44 | 0.820 |
| 43 | 0.750 |
| 42 | 0.690 |
| 41 | 0.630 |
| 40 | 0.570 |
| 39 | 0.520 |
| 38 | 0.480 |
| 37 | 0.430 |
| 36 | 0.390 |
| 35 | 0.360 |
| 34 | 0.330 |
| 33 | 0.300 |
| 32 | 0.270 |
| 31 | 0.250 |
| 30 | 0.220 |
| 29 | 0.200 |
| 28 | 0.180 |
| 27 | 0.170 |
| 26 | 0.150 |
| 25 | 0.140 |
| 24 | 0.120 |
| 23 | 0.110 |
| 22 | 0.100 |
| 21 | 0.090 |
| 20 | 0.080 |
| 19 | 0.060 |
| 18 | 0.050 |
| 17 | 0.040 |
| 16 | 0.030 |
| 15 | 0.030 |
| 14 | 0.030 |
| 13 | 0.020 |
| 12 | 0.020 |
| 11 | 0.020 |
| 10 | 0.020 |
| 9 | 0.010 |
| 8 | 0.010 |
| 7 | 0.010 |
| 6 | 0.010 |
| 5 | 0.010 |
| 4 | 0.010 |
| 3 | 0.010 |
| 2 | 0.010 |
| 1 | 0.010 |
| 0 | 0.000 |
At operator level 9 and lower, my DMM could not read any voltage so I just assumed it was a normalized level of about 0.01. Now resetting the operator levels to the normalized values as follows:
| Operator | Frequency | Level |
| 1 | 1.00 | 99 |
| 2 | 3.00 | 86 |
| 3 | 5.00 | 80 |
| 4 | 7.00 | 76 |
| 5 | 9.00 | 74 |
| 6 | 11.00 | 71 |
| 7 | 13.00 | 69 |
| 8 | 15.00 | 68 |
Then I got something that looked like
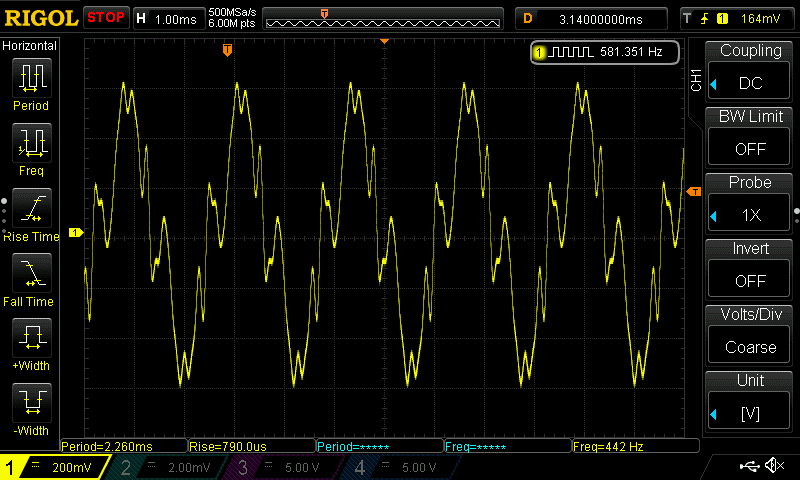
But that’s not a square wave – but it sounded like a square wave. The scope output looked like the operators were not in phase. After some investigation, I found that the operator frequencies drift. I was playing A440 on the keyboard and the Montage is tuned to 440.0Hz. I measured the frequency of a single sine wave on a DMM and found that the frequency would drift between 438Hz and 442Hz. I also confirmed there is no pitch modulation on the operator. I don’t know if this is intentional or an idiosyncrasy of the Montage OS version I am using which is version 3.50.0. When I reset the oscilloscope to trigger at the beginning of the sound, it looked like
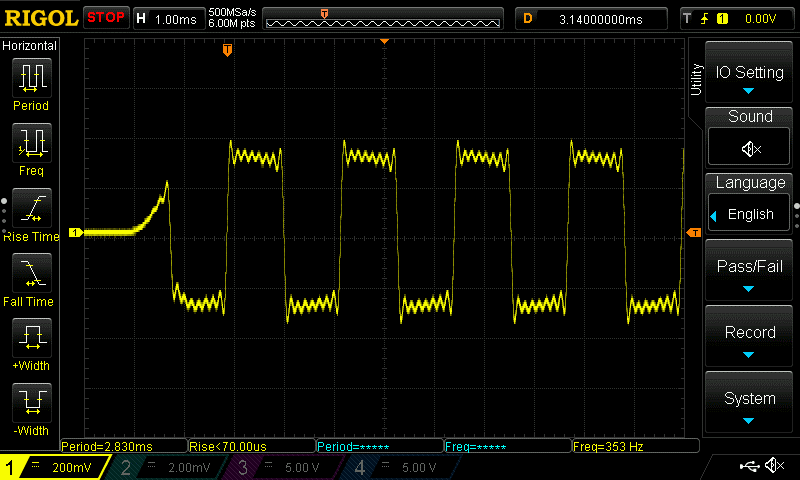
This looks very much like a square wave comprised of the first 8 partials. So we can safely assume that the operators are in sync in the beginning but drifts over time.
The Montage can generate up to 31 partials, so let’s try that. This can be accomplished with a performance with 2 FMX parts.
FMX Part 1
| Operator | Frequency | Level |
| 1 | 1.00 | 99 |
| 2 | 3.00 | 86 |
| 3 | 5.00 | 80 |
| 4 | 7.00 | 76 |
| 5 | 9.00 | 74 |
| 6 | 11.00 | 71 |
| 7 | 13.00 | 69 |
| 8 | 15.00 | 68 |
FMX Part 2
| Operator | Frequency | Level |
| 1 | 17.00 | 66 |
| 2 | 19.00 | 65 |
| 3 | 21.00 | 64 |
| 4 | 23.00 | 63 |
| 5 | 25.00 | 62 |
| 6 | 27.00 | 61 |
| 7 | 29.00 | 60 |
| 8 | 31.00 | 59 |
Here is what it looks like
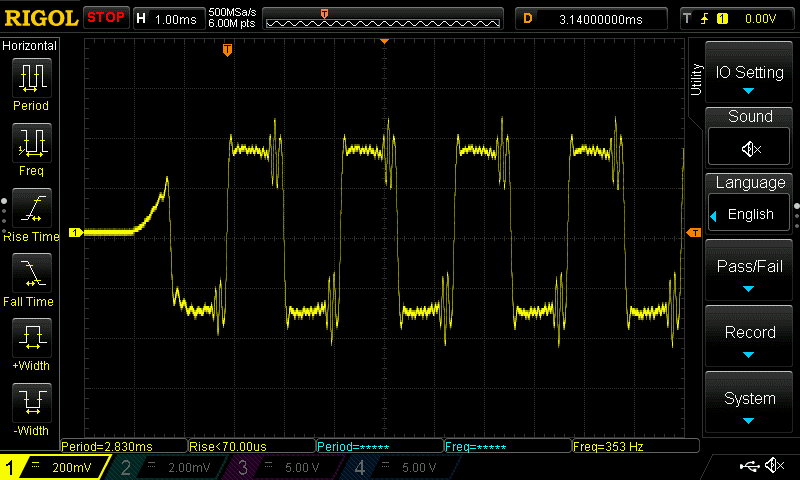
Is it a true square wave? No. It has some very some “ringing” in wave which I cannot explain. But when I compare it to the sampled square wave form (see below), it sounded the same to my ears. I can’t hear much over 12kHz so it might sound different to you.
We also know that FM synthesis can generate a “square” wave with 2 operators stacked with a 2:1 Carrier/Modulator frequency ratio.
Using any algorithm that has a 2 operator stack we can get square waves with varying degrees of “squareness”. It’s not really a true square wave but get’s pretty close. Here is the output of the waveform with various modulator operator output levels.
Modulator Output level is 67
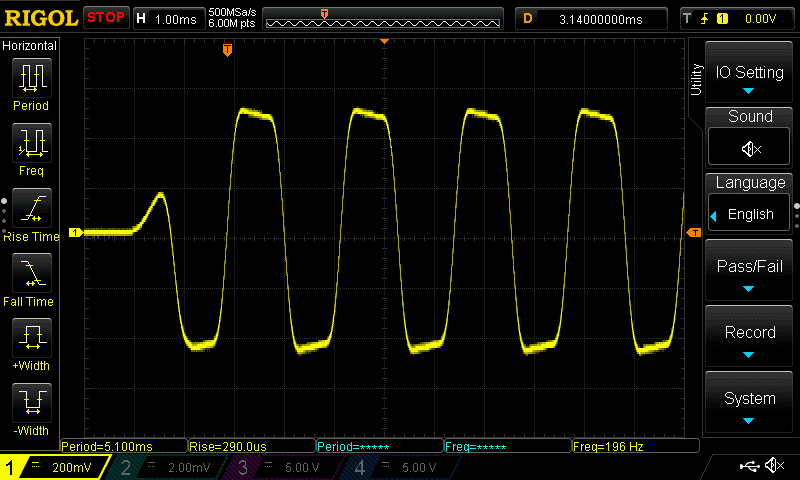
Modulator Output Level 72
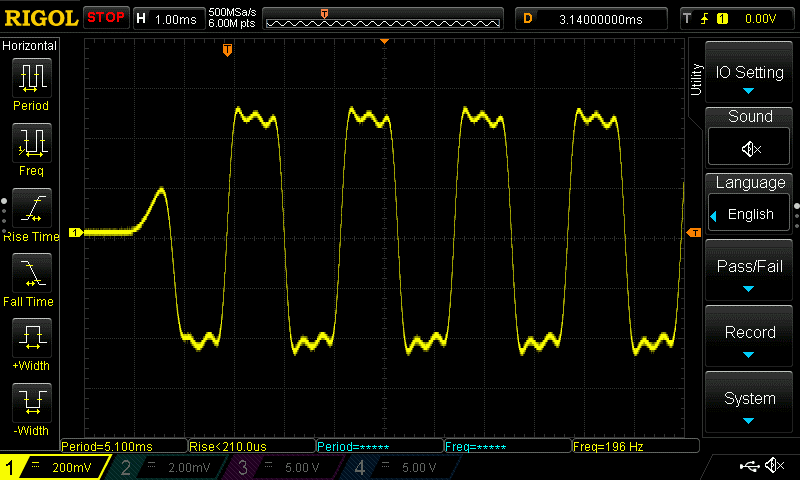
Modulator Output Level 75
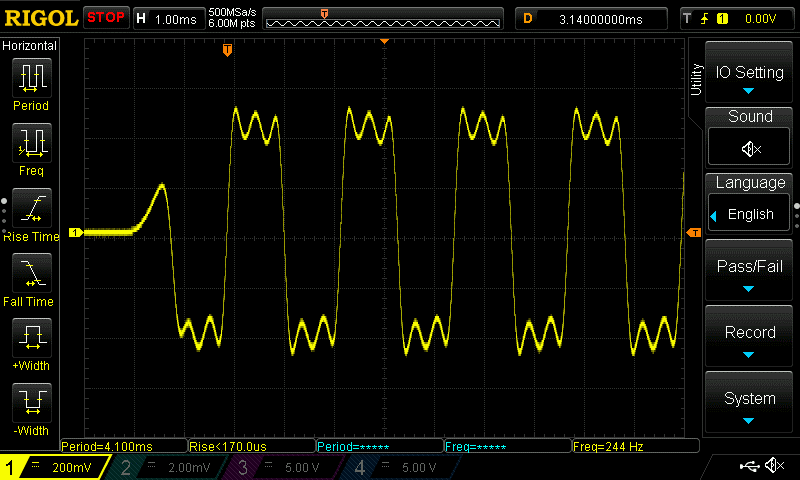
They look like square waves and sound like square waves but is not as bright as the squarewave generated with the additive synthesis.
The Montage has an AWM (sample based) synth engine also. If we look at the Synth waveforms, there is a square wave sample (#2136) called P50-1 which is a square wave with a 50% duty cycle and looks like.
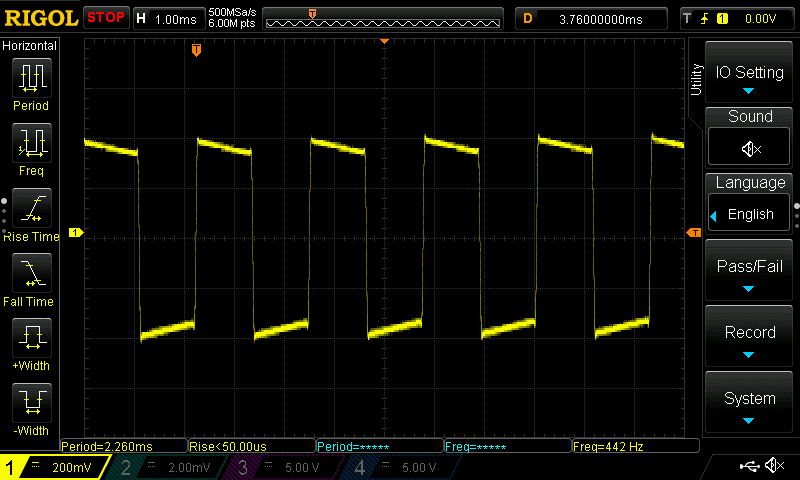
You can see it has the sharp pointy edges as you’d expect in a square wave but it had a bit of slope on the tops and bottoms which frankly surprised me. Regardless, it sounded the same as the square wave created with additive synthesis.
So, the Montage has 3 unique ways to generate waveforms like a square wave. Of course, the Montage has filters, effects, and a myriad of modulation sources which can be used to modulate these waveforms.